Para unir dos puntos con un trazo, podemos elegir un trazado recto o curvo. El trazado recto es único, pero existen infinidad de curvas entre dos puntos.
El simple trazado recto corresponde a la llamada curva de Bézier de grado 1 (o lineal), pero la cosa se anima para grados mayores. Las curvas de Bézier de grado mayor que 1 resultan extraordinariamente sencillas para crear trayectorias curvas entre dos puntos. Para construirlas, se interpola entre los extremos uno o más puntos. Cuantos más puntos interpolemos, de más grado (y posibilidades de control) será la curva. Por este motivo, los puntos interpolados se denominan puntos de control de la curva.
Pero simplemente interpolando uno o dos puntos de control (curvas de Bézier de grado 2 y 3) se obtienen resultados muy aceptables para una gran diversidad de situaciones. Por ejemplo, cada una de las letras de este texto (y casi cualquier otro que encuentres en una pantalla) ha sido diseñada usando curvas de Bézier cuadráticas y la mayoría de los gráficos vectoriales usan curvas de Bézier cúbicas.
Curvas racionales.
Una curva racional, también llamada curva unicursal, es una curva que es biracionalmente equivalente a una línea, que se puede tomar por una línea proyectiva e identificarla con el cuerpo de funciones racionales en una indeterminada F(x). Si F es algebraicamente cerrado, esto es equivalente a una curva de género cero; igualmente el cuerpo R(x,y) con x2+y2 = −1 es un cuerpo de género cero que no es una función cuerpo racional.
Curvas Spline.
Un spline es una curva diferenciable definida en porciones mediante polinomios.
En los problemas de interpolación, se utiliza a menudo la interpolación mediante splines porque da lugar a resultados sim
ilares requiriendo solamente el uso de polinomios de bajo grado, evitando así las oscilaciones, indeseables en la mayoría de las aplicaciones, encontradas al interpolar mediante polinomios de grado elevado.
Para el ajuste de curvas, los splines se utilizan para aproximar formas complicadas. La simplicidad de la representación y la facilidad de cómputo de los splines los hacen populares para la representación de curvas en informática, particularmente en el terreno de los gráficos por ordenador.
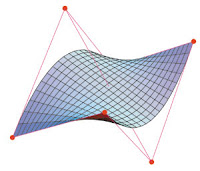
Superficies de Bezier.
Tienen las mismas propiedades que las curvas de Bézier y proporcionan un método conveniente para aplicaciones interactivas de diseño. Para especificar las posiciones de los puntos de control con coordenadas tridimensionales, podríamos en primer lugar construir una cuadrícula rectangular en el plano xy «de tierra»
Una superficie de Bézier compuesta construida con dos secciones de dos secciones de Bézier, unidas por la línea indicada, las líneas discontinuas unen los puntos de control, la continuidad de primer orden se establecen haciendo que la relación entre la longitud y la longitud z.



No hay comentarios:
Publicar un comentario